基础概念
在建模过程中,由于偏差过大导致的模型欠拟合以及方差过大导致的过拟合的存在,为了解决这两个问题,我们需要一整套方法及评价指标。其中评估方法用于评估模型的泛化能力,而性能指标则用于评价单个模型性能的高低。
泛化性能
模型的泛化性能是由学习算法的能力,数据的充分性及学习任务本身的难度所决定的,良好的泛化性能代表了较小的偏差,即算法的期望预测结果与真实结果的偏离程度,同时还要有较小的方差,即随训练样本的变化算法本身的学习能力变化不大。
模型评估方法
在模型评估中,我们经常要对数据集进行训练集和测试集的划分,数据集划分通常要保证两个条件:
- 训练集和测试集的分布要与样本真实分布一致,即训练集和测试集都要保证是从样本真实分布中独立同分布采样而得;
- 训练集和测试集要互斥,即两个子集之间没有交集。
基于划分方式的不同,评估方法可以分为:留出法,交叉验证法及自助法。
留出法
留出法是直接将数据集划分为两个互斥的集合,其中一个集合作为训练集,另一个作为测试集。另外需要注意的是在划分的时候要尽可能保证数据分布的一致性,避免因数据划分过程引入额外的偏差而对最终结果产生影响。 而当数据明显的分为有限类时,可以采用分层抽样方式选择测试数据,保证数据分布比例的平衡。
具体方法如下:
假设我们有数据集N,其中n个正样本,N-n个负样本,从正负样本中分别抽取比例为p的样本作为训练集的正负样本,其中训练集的正样本为np,负样本为(N-n)p,最后把剩下的样本n(1-p)作为测试集的正样本,(N-n)(1-p)作为测试集的负样本。同时,在数据集的划分比例差异不能太过悬殊,p太大会导致其训练结果和用整个数据集N训练的模型相近,p太小会导致模型的结果不稳定,即于整体样本N的训练结果差异过大。样本的不同划分方式会导致模型评估的相应结果也会有差别,例如如果我们把正样本进行了排序,那么在排序后的样本中采样与未排序的样本采样得到的结果会有一些不同,因此通常我们都会进行多次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
交叉验证法
交叉验证法(Cross Validation)的基础思路和留出法大致相同,都是讲数据集划分成训练集和测试集,而在划分细节上差异会比较大,而且交叉验证法还有诸多不同的分类形式。
Hold-Out Method
这个方法是将数据集随机分为两组,一组做为训练集,一组做为验证集,利用训练集训练模型,然后利用验证集验证模型,记录最后的分类准确率为此Hold-OutMethod下分类器的性能指标.此种方法的好处的处理简单,只需随机把原始数据分为两组即可,比留出法还要简单直接。
严格意义上来说,Hold-Out检验并不算是交叉检验,因为该方法没有达到交叉检验的思想,而且最后验证准确性的高低和原始数组的分类有很大的关系。
彻底的交叉验证
彻底的交叉验证(Exhaustive Cross Validation)是遍历全集N的所有子集n,把n作为训练集,N-n作为测试集,然后选择结果最好的那个,这种方法的时间复杂度太高,特别是数据集N很大的情况下,这种方法几乎是不可能完成的任务。
留P验证
留P验证(Leave-p-out Cross Validation)是把全集N中的p个样本作为测试集(p个样本遍历N中的所有可能组合),剩下的N-p个样本作为训练集,最终会得到N个模 型,用这N个模型最终的验证集的分类准确率的平均数作为此分类器的性能指标。这种方法从复杂度上看是比彻底交叉验证法简单了一些,但他的计算了依然非常大,因为p个元素的选择方法有n!/((n-p)!p!)个。当p=1的时候,叫留1验证(Leave-one-out Cross Validation),它的复杂度恰好是n。
k-折交叉验证
k-折交叉验证(K-fold Cross Validation)是把全集N分成K个相同大小的子集,遍历这k个集合,把当前被抽出的这个集合作为测试集,剩下的k-1个集合作为训练集,最终会得到k个模型,根据模型的结果统计,可以得到集合中测试错误的结果数量m。如果全集N的元素个数是n的话,可以得到该模型的错误率是E=(m1+m2+.....+mk)/n.
为了提高模型的精确度,可以将k-fold交叉验证的上述步骤重复t次,每一次都是随机划分全集N。在t次测试中,会得到t个模型的错误率E1,...,Et,最终的错误率为e=(E1+E2+...+Et)/t。
另外:当k=2时,称为2折交叉验证,k=n时,称为n着折交叉验证。
自助法
自助法(BootstrapMethod)在统计学上是一种有放回的抽样方法,不同于留出法和交叉验证法无放回的抽样方式。在做数据集分类时,如果我们对整体样本n进行n次有放回抽样得到n个样本,然后把抽到的n个样本作为训练集,其中会出现部分样本重复,同时有一部分样本一次也没被抽到,这部分作为测试集。
在有放回的n次抽样中,每次每个样本被抽中的概率为1/n,反过来,未被抽中的概率为1-1/n,进行n次抽样后,这个样本不被抽中的概率为1-1/n的n次方,当n的取值趋近于无穷大时,样本未被抽中的概率为e的负一次方,约等于0.368,因此可以认为测试集的样本大概会是整体样本的36.8%。
综述
根据以上不同方法的特点,在样本量较多的情况下一般选择留出法或交叉验证法来对数据进行分类,在样本较少的情况下采用自助法。
模型性能指标
混淆矩阵
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示。在机器学习的模型评价中用到的很多指标都来源于对混淆矩阵结果的运算。
下图是常见的二分类问题的混淆矩阵:
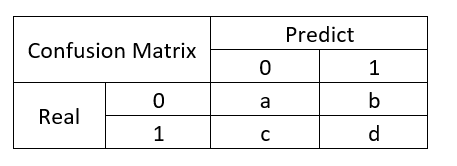
其中列表示模型预测值,行表示数据真实值。
根据图中的交叉结果会出现以下4种状况:
- 真实值为0,预测值也为0,用字母TP(True Positive)表示真正类数据。
- 真实值为0,预测值为1,用字母FN(False Negative)表示假反类数据。
- 真实值为1,预测值也为1,用字母TN(True Negative)表示真反类数据。
- 真实值为1,预测值为0,用字母FP(False Positive)表示假正类数据。
其中,True、False表示预测结果正确与否,Positive、Negative表示预测倾向为正类或者反类。
准确率、F1-Score、ROC曲线
整体分类结果的准确率accuracy=(TP+TN)/(TP+FN+TN+FP)
预测为正类的准确率,即在被预测为正类中真正是正类样本比例,又称精确率或查准率precision=TP/(TP+FP)
真实为正类的准确率,即在所有正类样本中被正确识别的比例,又称召回率或查全率TPR/recall=TP/(TP+FN)
F1-score是综合precision和recall两个指标的判断指标,
F1-Score=2/(1/precision+1/recall)=2precisionrecall/(precision+recall), F1-Score的值在0到1之间,越大越好。真实FP为负类预测错误率,即负类被预测为正类占所有真实负类的比例FPR=FP/(FP+TN)
ROC曲线是根据一系列不同的二分类方式(分界值或决定阈),以TPR为纵坐标,FPR为横坐标绘制的曲线。实际上ROC曲线是对一系列的TPR和FPR的值所构成点的连线绘制,而其中每一个点的都代表一个概率分界值,即把大于分界值得部分分为正类,小于分界值的分为负类。对于模型而言,我们计算出每个样本属于正类的概率,然后对概率值按顺序排序,计算每个概率作为分界点的TPR和FPR,然后绘制曲线,就构成了模型的ROC曲线。
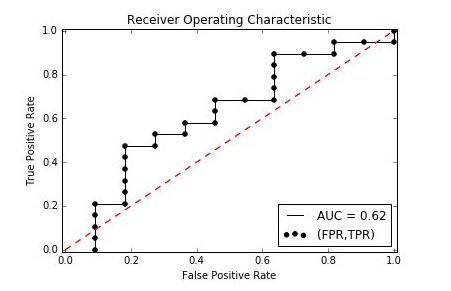
在样本有限的情况下,ROC曲线通常不是一条平滑的曲线,而是锯齿形的,数据较多的情况下,曲线会接近平滑。同时我们也可以通过计算 AUC(Area Under roc Cure)来做为评价指标。
参考资料:
《机器学习》——周志华